作者 | 叶永进、吴永正、兰冰、王石
摘要:近年来量子计算发展迅速,对很多行业特别是金融行业产生了变革性的影响,外汇市场将是第一个受到量子技术冲击的金融市场。我们提出一种量子套利优化方法,将货币兑换转化为二次无约束二元优化(QUBO)问题,利用量子退火算法求解汉密尔顿函数的最低能量态,实现高效的套利分析。传统的套利算法对于求解最佳套利交易路径是一个NP-hard问题,引入量子退火算法后,计算的时间复杂度大大降低,为解决该类问题提供了一条可行路径。该算法不仅可以得到最优解,还可以找到所有有利可图的交易路径,让交易者可以根据实际操作需要灵活地选择不同的交易路径。
关键词:套利;退火算法;量子计算
介绍
2020年10月16日下午,中共中央政治局就量子技术研究和应用前景举行第二十四次集体学习。中共中央总书记习近平在主持学习时强调,“当今世界正经历百年未有之大变局,科技创新是关键变量之一。我们要充分认识推动量子技术发展的重要性和紧迫性,加强量子技术发展的战略谋划和系统布局,把握大势,抢占先机”。随着量子技术时代的到来,量子计算、量子保密通信、量子测量等发展迅速。其中,量子计算凭借超强的并行计算能力,不断突破传统计算瓶颈,有望引领下一代科技革命。近年来,量子计算在国内外发展迅速,量子算法作为量子计算的应用方向,涉及各行各业,包括金融市场的应用。 本文重点关注量子算法在金融市场的创新研究,关注量子技术的大趋势,在量子金融领域先发制人。
量子金融概述
金融市场每天都会产生海量的交易数据,如何快速高效地处理这些数据对传统计算提出了巨大的挑战。量子计算以量子比特为基础,利用量子比特的纠缠和叠加特性,展现出超强的并行计算能力,在解决一些特定问题时具有巨大的加速效果,例如Shor算法在大数素因数分解过程中具有指数级加速[1],提出的搜索算法在无序集搜索问题中相对于经典算法具有二次方级加速[2]。因此人们希望将量子计算应用到金融领域,量子金融的概念也应运而生,即量子计算在金融领域的应用。目前,量子计算在金融领域的应用主要集中在金融交易、风险评估和金融工程等领域。量子计算在金融交易领域的应用是通过引入量子计算来指导金融交易,主要包括本文讨论的证券投资组合优化、股票价格预测和货币市场套利交易。 量子近似优化算法可以应用于证券投资组合,量子蒙特卡罗算法可以应用于股票价格预测,本文将量子退火算法应用于货币市场套利交易。在风险评估领域,量子计算主要应用于信用评分和欺诈检测。J. Egger 提出了一种用于信用评分的量子算法,Innan 提出了一种用于欺诈检测的量子图神经网络 [3]。量子金融工程主要是指将量子算法应用于金融衍生品的定价,包括期权定价等。量子蒙特卡罗算法也可以在这个方向发挥作用。
通过将量子算法与金融市场相结合,我们将传统的金融问题转化为具体的量子算法问题,利用量子计算机的特殊优势,突破传统计算的瓶颈,为我们提出的股票价格预测、投资组合优化、信用评估、外汇市场套利等金融问题提供快速有效的解决方案。
量子退火算法
以及二次无约束二元优化问题(QUBO)
组合优化是在离散域或可以简化为离散域的域中计算函数的最大值或最小值。日常生活中存在各种组合优化问题,例如商务旅行问题、交通流、班次规划等。此类问题通常包含大量可能的解,使得穷举搜索变得困难,因此需要寻求更快、更有效的计算方法。
为了克服这种计算限制,研究人员开发了一种名为伊辛机的新型计算技术。伊辛机是一种解决伊辛模型问题的机器。它将具体的数学问题转化为伊辛模型的结构欧易交易所,构造问题的汉密尔顿量,然后引入量子退火原理使汉密尔顿量绝热演化,使系统逐渐从激发态演化到基态,从而找到数学问题的最优解。在各个领域都进行了许多使用伊辛机的研究:投资组合优化[4]、流量优化[5]、电子商务网站的商品列表优化[6]和材料设计[7]。本文将伊辛机的应用扩展到货币交易市场的套利分析。
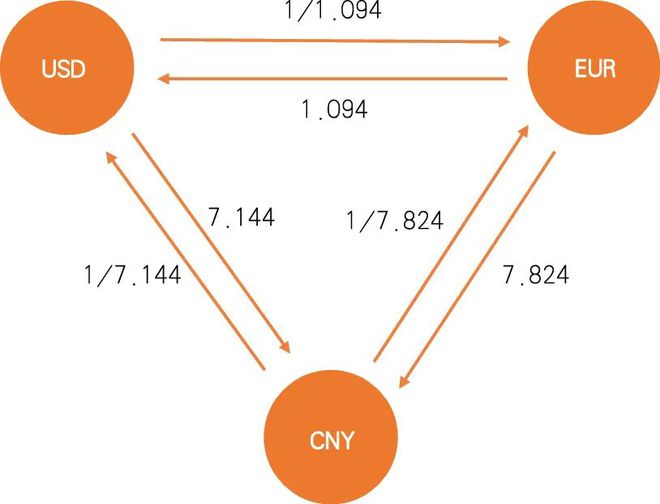
许多组合优化问题都可以在数学上转化为 Ising 模型或 QUBO 结构,并使用 Ising 机快速求解。Ising 模型和 QUBO 由图 G(V, E) 定义,其中 V 表示无向图的顶点,E 表示边。图 1 是货币套利交易的图 G(V, E) 的简单显示,其中节点(V)表示货币,边(E)表示货币之间的汇率。由于两种货币的汇率是不对称的,因此该图是有向图。
图1 美元(USD)、人民币(CNY)、欧元(EUR)货币兑换有向图
伊辛模型
在图G(V, E)中,伊辛模型哈密顿量表达式为:
其中,si为顶点i∈V上的自旋变量,hi为作用于i∈V上的外磁场,Jij为边(i,j)∈E上两顶点之间的耦合强度。
二次无约束二元优化问题 (QUBO)
QUBO 表示二次无约束二元优化问题,损失函数仅由一个线性项和一个二次项组成,具体表达式为:
其中xi为第i个二元变量,ai和bij均为实数。通过与Ising模型对比可知,Ising模型中的二元变量为si∈{-1,1},而QUBO中的变量为xi∈{0,1}。由于变量均为二元结构,因此Ising模型与QUBO本质上是相同的,可以通过系数相互转换。
货币套利分析
货币套利是指通过同一种货币在不同市场进行不同价格交易来获利的方式。如图1所示,图中汇率为2023年11月27日的实时汇率数据。例如100元人民币折算成美元,美元折算成欧元,欧元折算成人民币,折算后的人民币面值为:100×(1/7.144)×(1/1.094)×7.824≈100.11。经过一个周期的交易欧意交易所,人民币面值从100变成100.11,人民币面值升值0.11%,说明这一周期有套利空间,反之则无套利空间。
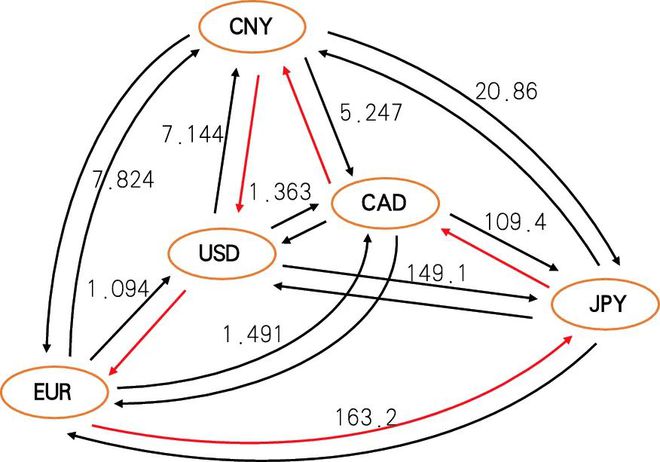
图2 人民币(CNY)、欧元(EUR)、美元(USD)、加元(CAD)、日元(JPY)五种货币交易路径图
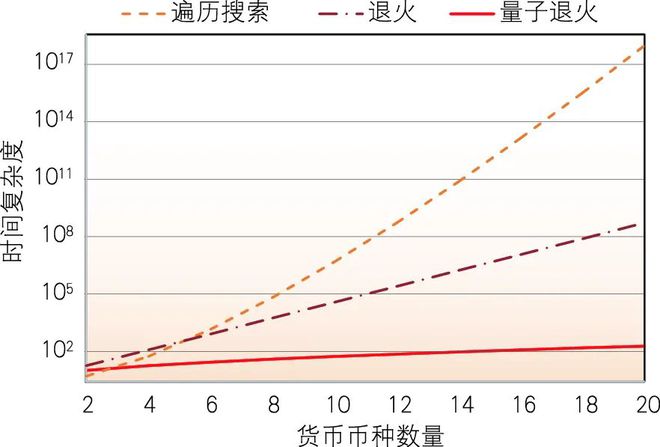
传统的套利分析是通过套利检测算法来实现的,即通过定义一个如图2所示的有向图,对有向图中的任意一个环,计算环内汇率的乘积,然后取对数并乘以-1,即-log(ΠRij),其中Rij表示货币i对货币j的实时汇率。当(ΠRij)>1时,认为该环有利可图,有套利空间,否则无套利空间。在有套利空间的闭环中,-log(ΠRij)的值为负数,简称负环。套利检测算法就是在图中寻找负环,找到第一个负环后就停止寻找。 传统的套利检测算法可以在多项式时间内求解,例如时间复杂度为 O(|V||E|)(其中 |V| 为节点数,|E| 为边数)的 -Ford 算法,以及时间复杂度为 O(|V|3) 的 Floyd 算法。这些算法的特点是,在找到第一个负循环后终止搜索。相反,要找到最有利可图的套利机会,则需要遍历并搜索图中所有的循环。遍历搜索的时间复杂度为 O(|V|!),这是一个 NP-hard 问题。
在实际交易中,交易者会更关注交易模型,会综合考虑交易方式、市场流动性、交易周期短、风险小等因素。比如有两个交易计划,一个是小幅盈利,一个是巨额盈利。一般传统的交易算法,比如福特算法、弗洛伊德算法,在找到第一个盈利的交易计划后就停止搜索。我们本文提供的量子退火算法,不仅可以找到最赚钱的交易计划,还可以按照盈利顺序给出多个其他交易计划,让交易者在实际交易中选择最可行的交易路径。
对于一般情况,假设有N种货币,构造一个有N个节点(V)和N×(N-1)条边(E)的有向图。令Rij表示货币i对货币j的汇率。实际交易过程中,需要考虑兑换交易的中介费用,将中介费用成本折算成汇率即可。由于本文只讨论算法的有效性,因此暂时不考虑中介费用。定义二元变量xij:
这个优化问题的目标是在有向图中找到最赚钱的交易环。即在一个闭环中,经过一个交易周期后,选取ΠRij的最大值(闭环内所有Rij)。为了更一般的表示,需要引入一个二元变量xij,即寻找Π[(Rij-1)xij+1]的最大值。从数学上讲,乘法可以通过取对数变成加法,因此我们的目标函数简化为:
因为我们的交易要闭环完成,那么闭环必须满足两个条件:第一,在图中节点处,如果处于交易循环中,会有一个货币兑换输入,也会有一个货币兑换输出,用数学上可以表示为:
如果图中节点不在闭环中,则输入和输出数字均为 0,自动满足上述等式。其次,如果图中节点在闭环中,则有且仅有一个兑换输出,满足上述等式。如果节点不在闭环中,则没有与任何其他节点进行货币兑换,满足上述等式。结合这两项,我们得到第二个约束:
通过确定目标函数和两个约束条件,可以构造出系统的目标哈密顿量。由于量子退火算法的固有特点是从激发态通过绝热演化找到系统的基态,因此将上述目标函数乘以-1,并加入两个约束条件,即可得到系统的哈密顿量:
其中,α、β为系统哈密顿量的超参数,其值为正数,参数值越大,表示在退火演化过程中的约束越强,具体值可根据程序运行效率和结果适当调整。
在确定了系统的哈密顿量之后,再利用前面介绍过的伊辛机模拟量子退火过程,就能很快求解出系统的最低能态,也就是最优化问题的最优解。
结果与讨论
本文采用DWave开发的模拟退火模块实现量子退火模拟操作。根据前面的介绍,只要给出二元二次哈密顿量,就可以完成量子退火的模拟计算。本文采用2023年11月27日人民币、欧元、美元、加元、日元五种货币的实时汇率数据作为模拟计算输入,如图2所示。图中数字为当日汇率,图中只标注了一半汇率数据,另一半可以取反(如USD→CNY汇率为7.144,CNY→USD汇率为1/7.144)。
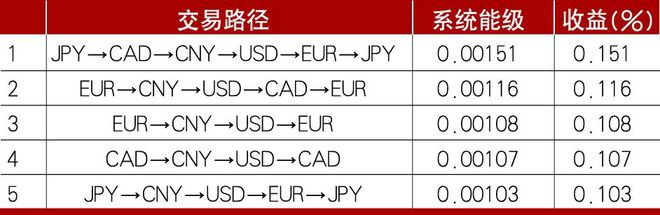
表1 利用量子退火算法求解的最优5条交易路径
通过量子退火算法的计算,系统能级最低对应的量子态就是我们需要的最优解。表1列出了5个系统能级最低,对应5条最优交易路径。图2中红色箭头表示最优解。表1中的能量就是系统汉密尔顿量对应的能级。通过量子退火算法,我们找到了最赚钱的交易路径,即“JPY→CAD→CNY→USD→EUR→JPY”。通过这条路径进行交易,每笔交易可以实现0.151%的闭环盈利。这种方法不仅可以提供最优交易路径,还可以给出其他交易路径,包括系统绝热演化过程中经历的所有交易路径。为了方便,这里只列出了排名前五的交易路径。所有盈利路径的解可以让交易者在实际交易过程中根据交易成本、市场流动性、更短的闭环等进行灵活选择。
图3 货币套利交易中不同算法的时间复杂度
结论
本文将量子退火算法的应用拓展到货币交易市场,利用量子算法超强的并行计算能力解决传统的NP-hard问题,为货币交易市场打开了一扇新的大门。随着金融科技的发展,量子计算在金融领域的广泛应用,传统金融市场将受到冲击,一些传统范围内无法解决的问题,可能被量子计算所突破,从而带来金融领域的一场新变革。我们正站在伟大时代的前沿,将量子技术引入金融领域,将给我们带来一个全新的金融世界。
【参考】
[1]Shor PW.量子计算算法:离散对数和量子纠缠[J].1994年第35期:124-134.
[2] G rover LK. AFS 量子计算[J]. 第 28 届 ACM 进展, 1996: 212-219
[3] Innan、Ashim Dhor 等人。 利用图进行欺诈[J]. 2023 年。
[4]G.,P.,P. G 等. 使用退火算法求解最优问题[J]. IEEE of , 2016, 10(6): 1053- 1060.
[5]F. , G. , C.等. Fow的使用[J]. 信息与通信技术, 2017, 4: 1-6.
[6]N. , K. , K. 等. 基于电子商务网站的商品分析[J]. ,2019年。
[7]K. Kitai, J. Guo, S. Ju, 等. 与和[J]. 物理评论研究, 2020, 2 ( 1 ): 1910.
[8] S, B.:和[J]. The. 2015. 224(1): 17-24。
作者单位:中国电子科技集团公司第三十二研究所



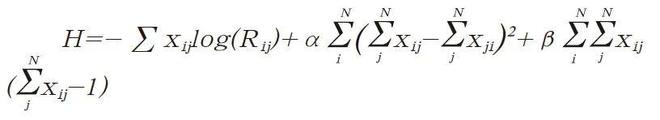


网友评论